奇偶相乘，函数结果大

在数学领域中，函数是描述变量之间关系的重要工具。根据函数的性质，我们可以将它们分为奇函数、偶函数和其他类型的函数。奇函数和偶函数因其独特的对称性而备受关注。本文将深入探讨一个有趣的问题：奇函数乘以偶函数等于什么？

一、奇函数与偶函数的定义

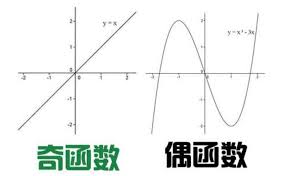
首先，我们需要明确奇函数和偶函数的定义：

- 奇函数：如果对于函数$f(x)$，有$f(-x) = -f(x)$对所有在其定义域内的$x$都成立，那么$f(x)$是奇函数。例如，$f(x) = x^3$就是奇函数。

- 偶函数：如果对于函数$g(x)$，有$g(-x) = g(x)$对所有在其定义域内的$x$都成立，那么$g(x)$是偶函数。例如，$g(x) = x^2$就是偶函数。

二、奇函数与偶函数的性质

奇函数和偶函数具有一些显著的数学性质，这些性质在解题时非常有用：

- 奇函数的图像关于原点对称：即，图像在$x$轴上方和下方的部分是关于原点对称的。

- 偶函数的图像关于$y$轴对称：即，图像在$y$轴的左侧和右侧的部分是关于$y$轴对称的。

- 奇函数在$x=0$处的值为0（如果0在其定义域内）：这是因为$f(0) = -f(0)$，唯一满足这一条件的数是0。

- 偶函数在$x=0$处的值可能是任意实数：因为$g(0) = g(0)$，不产生矛盾。

三、奇函数乘以偶函数的结果

现在，我们来分析奇函数乘以偶函数的结果。设$h(x) = f(x) ⁄⁄cdot g(x)$，其中$f(x)$是奇函数，$g(x)$是偶函数。

1. 对称性分析：

- 由于$f(x)$是奇函数，其图像关于原点对称。

- 由于$g(x)$是偶函数，其图像关于$y$轴对称。

- 当我们将两者相乘时，由于奇函数和偶函数的对称性，$h(x)$的图像将不再具有关于原点或$y$轴的对称性。

2. 奇偶性分析：

- $h(-x) = f(-x) ⁄⁄cdot g(-x)$

- 由于$f(-x) = -f(x)$且$g(-x) = g(x)$，代入上式得：

$h(-x) = -f(x) ⁄⁄cdot g(x) = -h(x)$

- 这表明，$h(x)$既不是奇函数（因为$h(-x) ⁄⁄neq h(x)$），也不是偶函数（因为$h(-x) ⁄⁄neq -h(x)$）。我们称这样的函数为非奇非偶函数。

3. 具体例子：

- 设$f(x) = x$（奇函数）和$g(x) = x^2$（偶函数）。

- 则$h(x) = f(x) ⁄⁄cdot g(x) = x ⁄⁄cdot x^2 = x^3$。

- 但这里需要注意，虽然$h(x) = x^3$看起来像一个奇函数，这是因为我们选择的$f(x)$和$g(x)$恰好使得$h(x)$的形式保持为奇函数。在一般情况下，奇函数乘以偶函数的结果将是一个非奇非偶函数。

四、结论

综上所述，奇函数乘以偶函数的结果是一个非奇非偶函数。这一结论基于奇函数和偶函数的定义及其对称性质。通过具体的例子，我们可以进一步验证这一结论。在数学学习和研究中，了解不同类型的函数及其性质对于解决问题至关重要。希望本文能帮助读者更好地理解和应用奇函数和偶函数的概念。